3 Analyse op basis van voxels
3.1 Analyse rond de windturbines
Een voxel is het driedimensionale equivalent van een pixel. Het is een balk met bepaalde breedte, lengte en hoogte. Voor de eenvoud definiëren we de voxel als een kubus met zijde 30 m.
Rond elke windturbine creëren we een raster van 21 voxels in elke richting. Per voxel tellen we het aantal tracks dat door de voxel gaat. Het aantal tracks per voxel is dan een maat voor de activiteit van vogels in de voxel. Onze hypothese is dat de activiteit van de vogels afhangt van de positie ten opzichte van de windturbine en van de windrichting. Om rekening te houden met de windrichting kozen we om de vogeltracks te roteren rond de positie van de windturbine zodat alle geroteerde tracks schijnbaar zuidenwind hebben. Op die manier kijken we naar de relatieve positie van de tracks ten opzichte van het rotorvlak. Bij zuidenwind is het rotorvlak oost - west georiënteerd. In figuur 3.1 geven we een voorbeeld waarbij we zowel de originele track met bijhorende windrichting weergeven als de geroteerde versie. We centreren het voxelgrid op de voet van de windturbine. Een positieve y-waarde is dan het gebied windafwaarts van de windturbine.
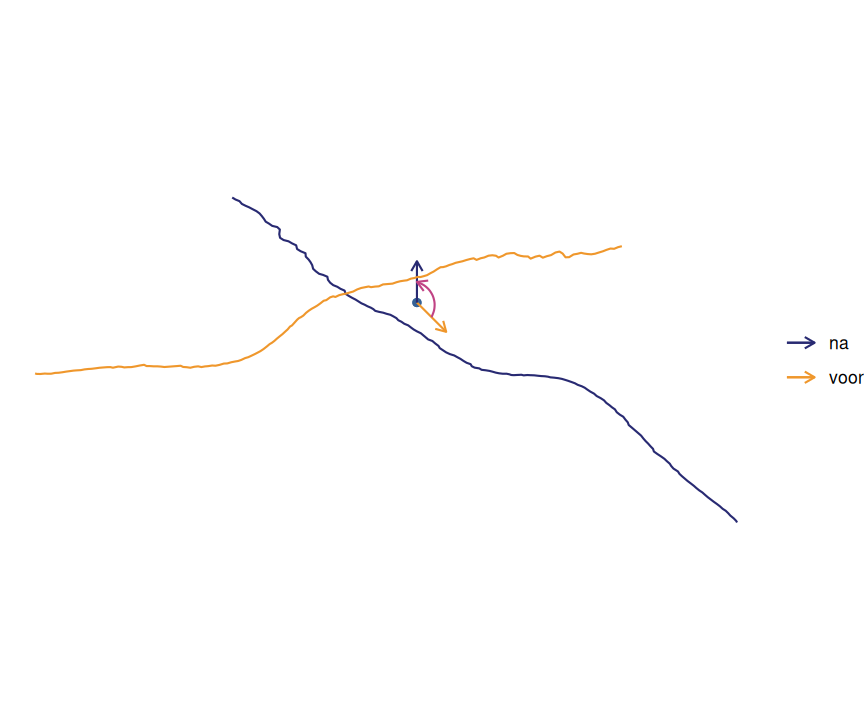
Figuur 3.1: Voorbeeld van een track (lijn) en de bijhorende windrichting (pijl) voor en na de rotatie. De fushia pijl geeft de draairihcting weer.
We berekenen het voxelgrid rond alle windturbines in de buurt van de radar. We weerhouden enkel de windturbines waar de som van het aantal tracks per voxel over alle voxels minstens 5% van de windturbine met het hoogste aantal tracks lager dan 200 m bedraagt (fig. 3.2). Dit criterium vermijdt dat we windturbines gebruiken waar de radar te weinig zicht heeft op lage hoogte. Hoe groter de afstand tussen de radar en de windturbine, hoe groter de kans dat de radar onvoldoende zicht heeft op lage hoogte. De windturbines in figuur 3.2 zijn alle windturbines die beschikbaar zijn in OpenStreetMap in de omgeving van de Antwerpse haven. In de omgeving staan een aantal kleinere windturbines. Voor deze analyse beperken we ons tot de turbines met minstens 1 MW vermogen. Indien OpenStreetMap geen informatie bevat over het vermogen, dan hebben we turbine alsnog gebruikt in de analyse.

Figuur 3.2: Gebruikte windturbines voor analyse met aanduiding van de regio van het voxelraster.
In figuur 3.3 tonen we de som over alle relevante windturbines. Elke deelfiguur toont een horizontale snede op een bepaalde hoogte. De meeste activiteit speelt zich af tussen 270 en 450 m. Dat is een zone boven het rotorvlak van de windturbines. Eventuele andere patronen in de figuur zijn minder duidelijk door het sterke verschil in activiteit tussen de verschillende hoogtes.
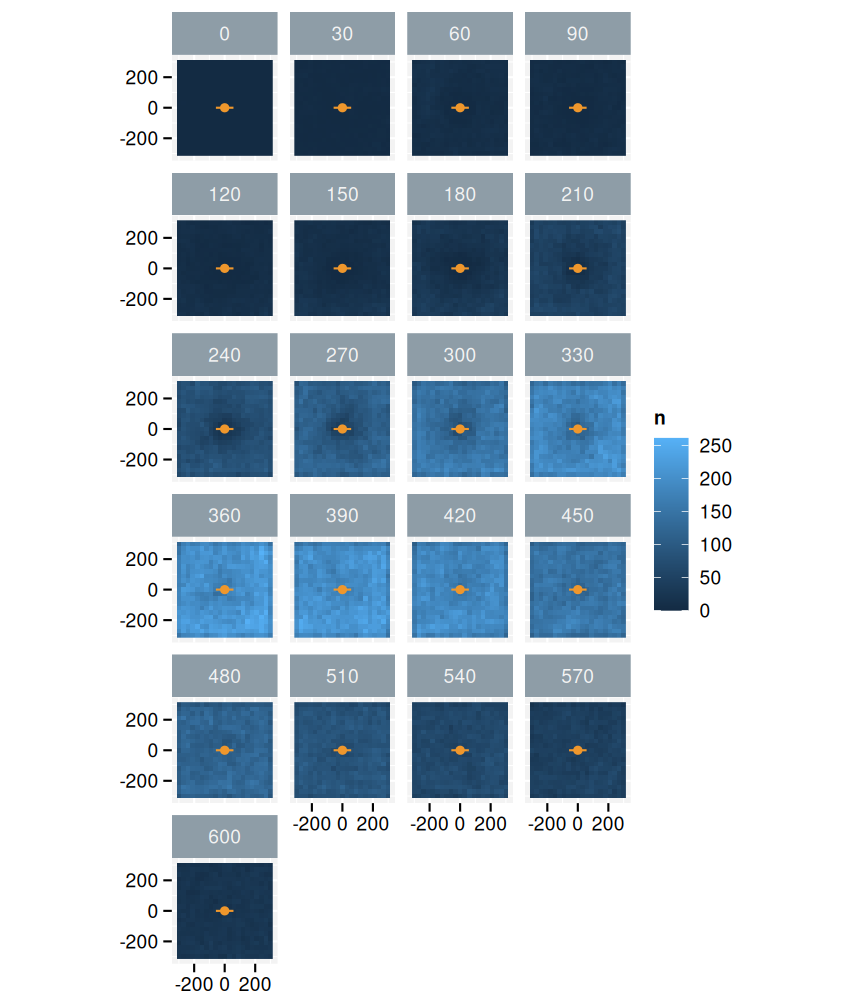
Figuur 3.3: Overzicht van het totaal aantal tracks per voxel over alle geselecteerde windturbines. In oranje geven we de positie van de mast en rotor weer in 2 dimensies. De deelfiguren geven de verschillende hoogtes weer.
Om beter zicht te krijgen op de patronen, modelleren we ze met behulp van een statistisch model.
De activiteit \(Y_{ixyz}\) in voxel \(xy\) in snede \(z\) rond windturbine \(i\) volgens een Poisson verdeling met gemiddelde \(\mu_{ixyz}\) (3.1).
Dit gemiddelde \(\mu_{ixyz}\) is met een \(\log\) link gekoppeld aan de lineaire predictor \(\eta_{ixyz}\) (3.2).
De lineaire predictor \(\eta_{ixyz}\) hangt af van het globaal gemiddelde \(\beta_0\), het effect \(b_i\) van de windturbine \(i\), het effect van de hoogte \(b_z\) en het gemiddelde effect \(\xi(xy,z)\) van de voxel \(xy\) in laag \(z\).
We veronderstellen dat het windturbine effect uit een Gaussiaanse verdeling met gemiddelde \(0\) en standaard afwijking \(\sigma_w\) (3.4).
Het effect van de hoogte modelleren we als een tweede orde toevalsbeweging (second order random walk) (3.5).
Het effect van de voxel \(\xi(xy,z)\) modelleren we als horizontale lagen die een Gaussian Markov Random Field (GMRF) volgen waarbij twee boven elkaar gelegen lagen een autogressief model van order 1 volgen (3.6).
Het model schat de correlatie tussen twee boven elkaar gelegen lagen op 0.914 (0.896; 0.929).
Het GMRF zorgt voor een ruimtelijke autocorrelatie in het horizontale vlak volgens een Matern covariantie functie.
\[\begin{equation} Y_{ixyz} \sim \mathcal{P}\mbox{oisson}(\mu_{ixyz}) \tag{3.1} \end{equation}\] \[\begin{equation} \log(\mu_{ixyz}) = \eta_{ixyz} \tag{3.2} \end{equation}\] \[\begin{equation} \eta_{ixyz} = \beta_0 + b_i + b_z + \xi(xy,z)\tag{3.3} \end{equation}\] \[\begin{equation} b_i \sim \mathcal{N}(0, \sigma_w)\tag{3.4} \end{equation}\] \[\begin{equation} \Delta_z^2 = (b_{z + 1} - b_z) - (b_z - b_{z - 1}) \\ \Delta_z^2 \sim \mathcal{N}(0, \sigma_z)\tag{3.5} \end{equation}\] \[\begin{equation} \xi(xy,z) = a \xi(xy, z - 1) + w(xy, z)\tag{3.6} \end{equation}\]
In figuur 3.4 geven we het effect van de windturbine. Het verschil tussen de windturbine met hoogste en laagste activiteit is begrenst omdat we enkel de windturbines gebruiken die minstens 10% van de activiteit van de windturbine met hoogste activiteit hebben. De positie van de radar zal voor een belangrijk deel dit effect verklaren. De radar heeft immers een beperkt bereik. Afhankelijk van de afstand tussen de radar en de windturbine zal de radar meer of minder tracks kunnen waarnemen.
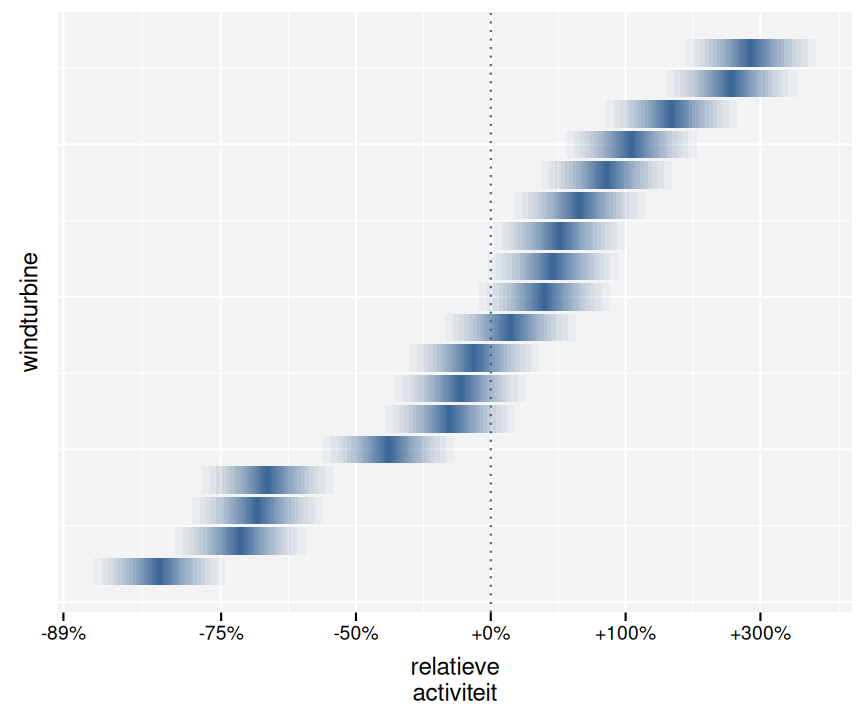
Figuur 3.4: Gemiddelde activiteit per windturbine. Relatief ten opzichte van de globaal gemiddelde activiteit.
Zoals we reeds konden verwachten op basis van figuur 3.3, stellen we een sterk effect volgens de hoogte vast (fig. 3.5). Tussen 200 en 600 m hoogte stellen we een hoger dan gemiddelde activiteit vast met een piek rond 400 m. Onder de 100 m stellen we een sterke afname van de activiteit vast. Dit is mogelijk te wijten aan beperkingen qua zichtbaarheid door de radar.
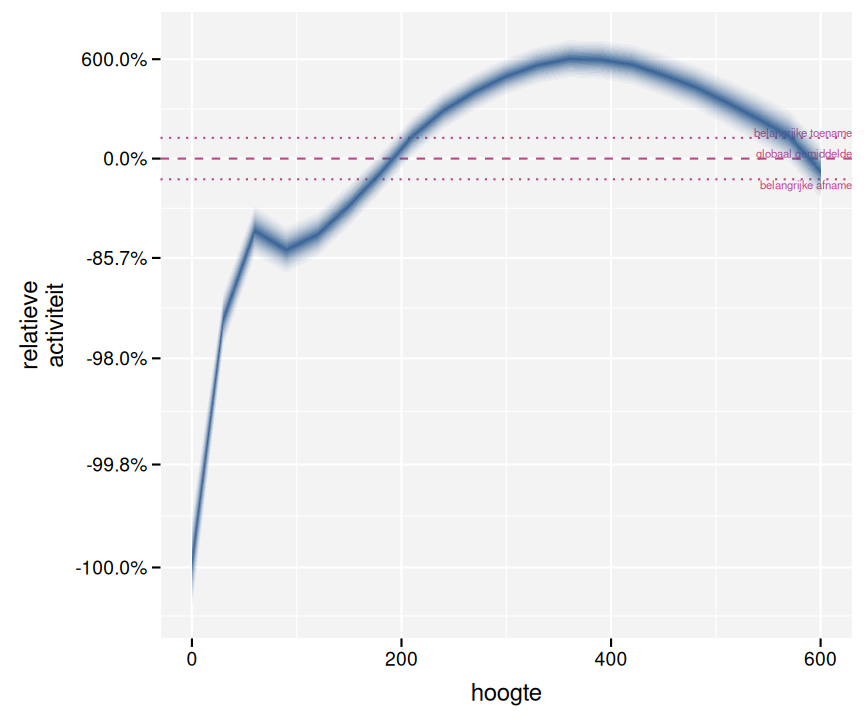
Figuur 3.5: Effect van de hoogte op de relatieve activiteit. Relatief ten opzichte van de globaal gemiddelde activiteit.
Ten slotte hebben we nog het effect van de voxels, na de correctie voor het effect van de windturbine en de hoogte. Figuur 3.6 toont twee verschillende patronen. Boven 330 m zien we relatief weinig verschillen tussen verschillende posities in de horizontale vlakken. Tussen 90 en 210 m stellen we een sterk patroon vast in de horizontale lagen. Vlakbij de windturbine is de activiteit beduidend lager dan rond de windturbine. Merk op dat het bereik van de daling in activiteit min of meer overeenkomt met het rotorvlak. De zone met lagere activiteit lijkt windafwaarts van de windturbine (bovenrand van de figuur) iets groter te zijn dan windopwaarts van de windturbine.

Figuur 3.6: Gemiddelde activiteit in de omgeving van een windturbine. Relatief ten opzichte van de gemiddelde activiteit op die hoogte.
3.2 Vergelijkbare analyse in de omgeving van windturbines
Om na te gaan wat de mogelijke invloed van de windturbine is, herhalen we de analyse voor locaties zonder windturbine. We generen een set van aselecte punten in de omgeving van windturbine zodat de voxelrasters van de controlepunten dichtbij de windturbine zijn, zonder overlap tussen de voxelrasters (fig. 3.7). Ook hier weerhouden we enkel de controlepunten waarvan de activiteit op hoogste 200 m minstens 5% bedraagt van de windturbine met hoogste activiteit onder 200 m. De controlepunten bestaat uit 12 punten, terwijl de originele set uit 18 punten bestaat.
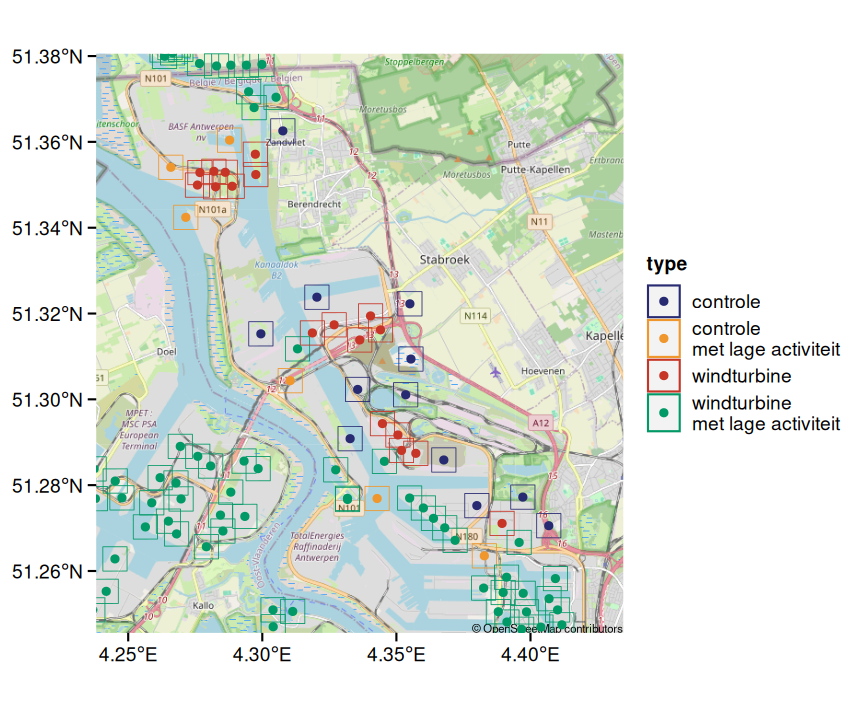
Figuur 3.7: Aselecte controle punten nabij gebruikte windturbines. Kandidaat verwijst naar controle punten met te weinig activiteit.
Wanneer we naar de ruwe gegevens van de controlepunten kijken stellen we opnieuw een sterk effect van de hoogte vast (fig. 3.8). Om een betere vergelijking te kunnen maken, fitten we hetzelfde statistisch model aan de controlepunten.
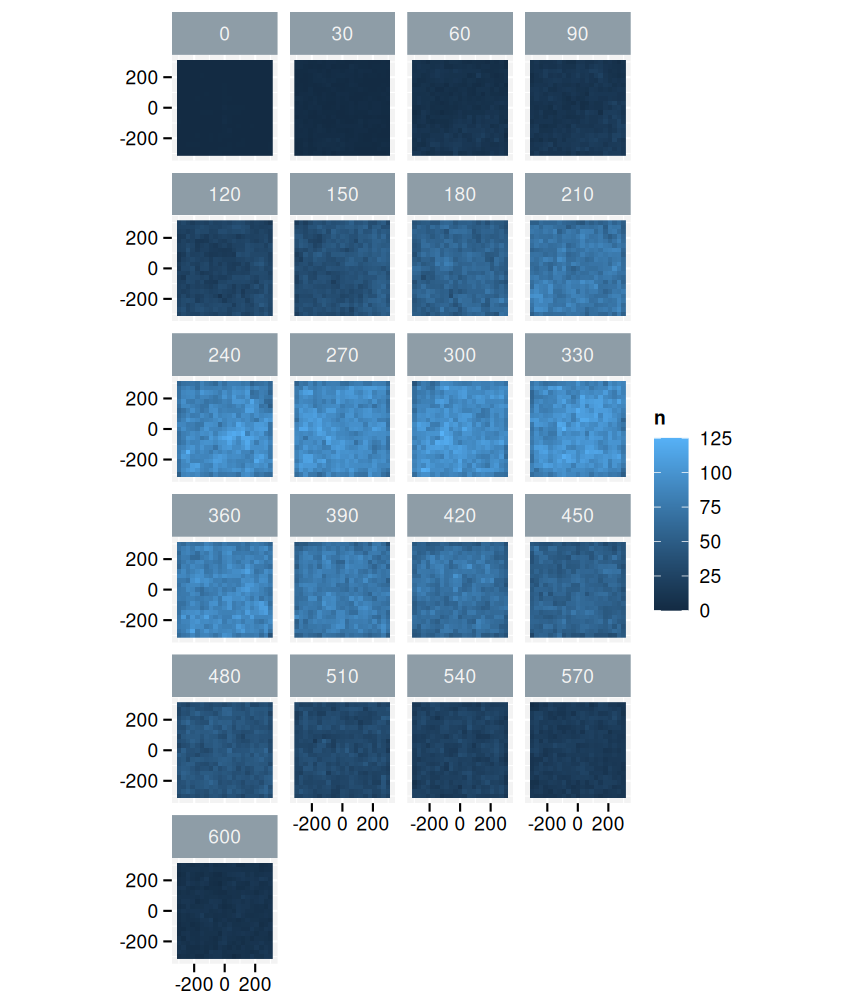
Figuur 3.8: Overzicht van het totaal aantal tracks per voxel over willekeurige punten in de buurt van windturbine. De deelfiguren geven de verschillende hoogtes weer.
In eerste instantie kijken we naar de hyperparameters van het model. Dit zijn de parameters die de variabiliteit van de verschillende componenten van het model bepalen. Bij de controlepunten stellen we minder sterke correlaties vast (tabel 3.1). De correlatie tussen de horizontale lagen daalt van \(0.90\) naar \(0.79\). De afstand waarover de horizontale autocorrelatie een rol speelt daalt van 460 m naar 320 m. De sterke van de horizontale autocorrelatie halveert. De verschillen tussen de controle punten daalt met een derde. Enkel de variabiliteit van het hoogte-effect verdubbelt nagenoeg. Het hoogte-effect beschrijven we met een tweede orde toevalsbeweging. Een kleine variantie van een tweede orde toevalsbeweging zorgt voor een geleidelijk patroon. Naarmate de variantie groter is, is het patroon flexibeler.
| parameter | windturbine | controle |
|---|---|---|
| Correlatie tussen horizontale lagen | 0.914 (0.896; 0.929) | 0.840 (0.800; 0.875) |
| Afstand ruimtelijke autocorrelatie | 620 (490; 800) | 330 (280; 400) |
| Variantie ruimtelijke autocorrelatie | 0.113 (0.071; 0.178) | 0.032 (0.024; 0.043) |
| Variantie punten | 0.77 (0.40; 1.41) | 0.65 (0.29; 1.34) |
| Variantie hoogte | 0.83 (0.38; 1.67) | 0.13 (0.06; 0.24) |
Bij de windturbine stellen we gemiddelde een lagere activiteit vast (-30% (-70%; +60%), fig. 3.9).
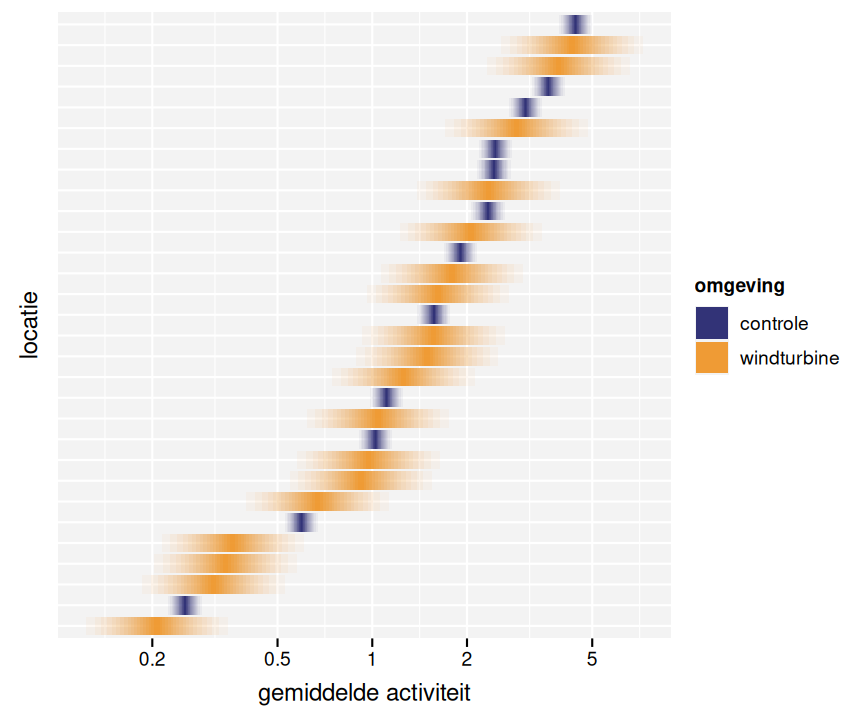
Figuur 3.9: Gemiddelde activiteit per locatie.
Het patroon van het hoogte effect verschilt eveneens (fig. 3.10). Rondom windturbine lijkt er een lagere activiteit te zijn onder 250 m en een hogere activiteit daarboven.

Figuur 3.10: Gemiddelde activiteit in functie van de hoogte. Relatief ten opzichte van de globaal gemiddelde activiteit.
Het verschil bij de voxels is spectaculair. Waar we rond de windturbines op lage hoogte (tot 300 m) sterke patronen vast stellen (fig. 3.6), zijn deze bij de controlepunten slechts in beperkte mate aanwezig (fig. 3.11). De kleurgradiënt in beide figuren gebruikt dezelfde kleurschaal zodat we ze gemakkelijk met elkaar kunnen vergelijken.
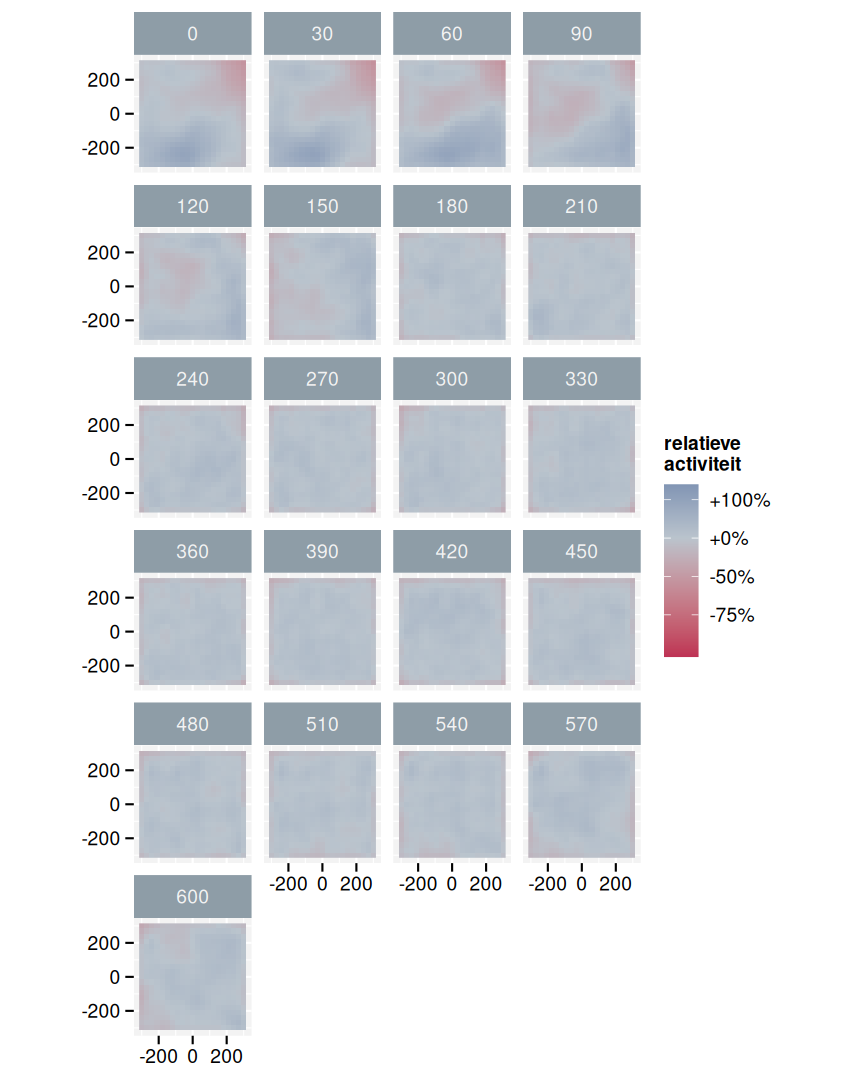
Figuur 3.11: Gemiddelde activiteit in de omgeving van een controlepunt. Relatief ten opzichte van de globaal gemiddelde activiteit.
3.3 Relatief verschil tussen beide modellen
In deze sectie kijken we naar de verschillende in voorspelde waarde tussen beide modellen. Kijken we enkel naar de globale verschillen dan blijkt de activiteit rond windturbines gemiddeld -30% (-70%; +60%) te bedragen van de activiteit rond de nabijgelegen controlepunten.
Boven 300 m stellen we geen significant verschil in relatieve activiteit vast (fig. 3.12). Onder 240 m stellen we rond de windturbines een sterke significante afname van de relatieve activiteit vast.
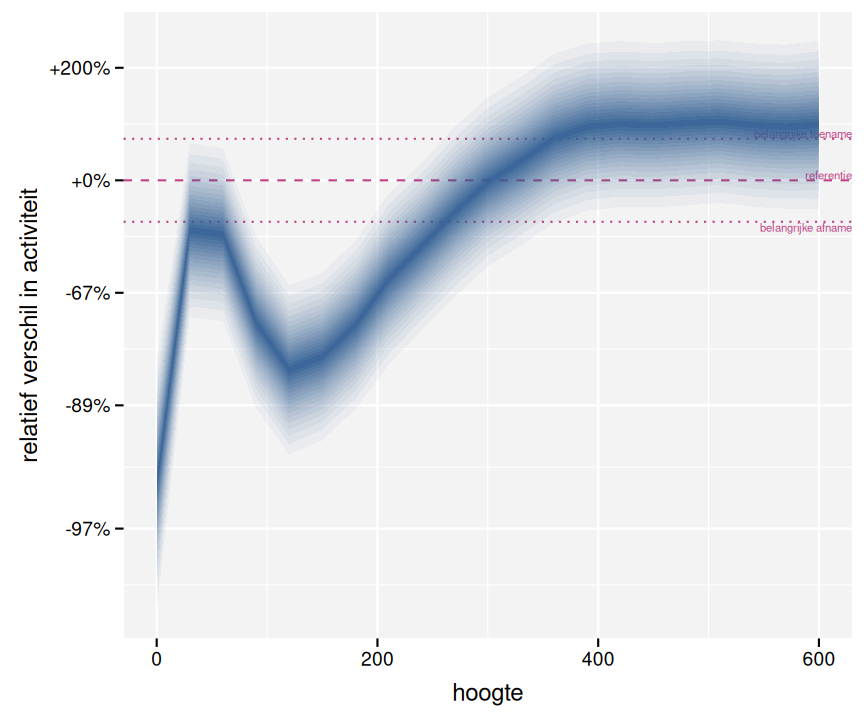
Figuur 3.12: Verschil in relatieve activiteit per hoogte rond windturbines versus rond controlepunten in de omgeving van windturbines.
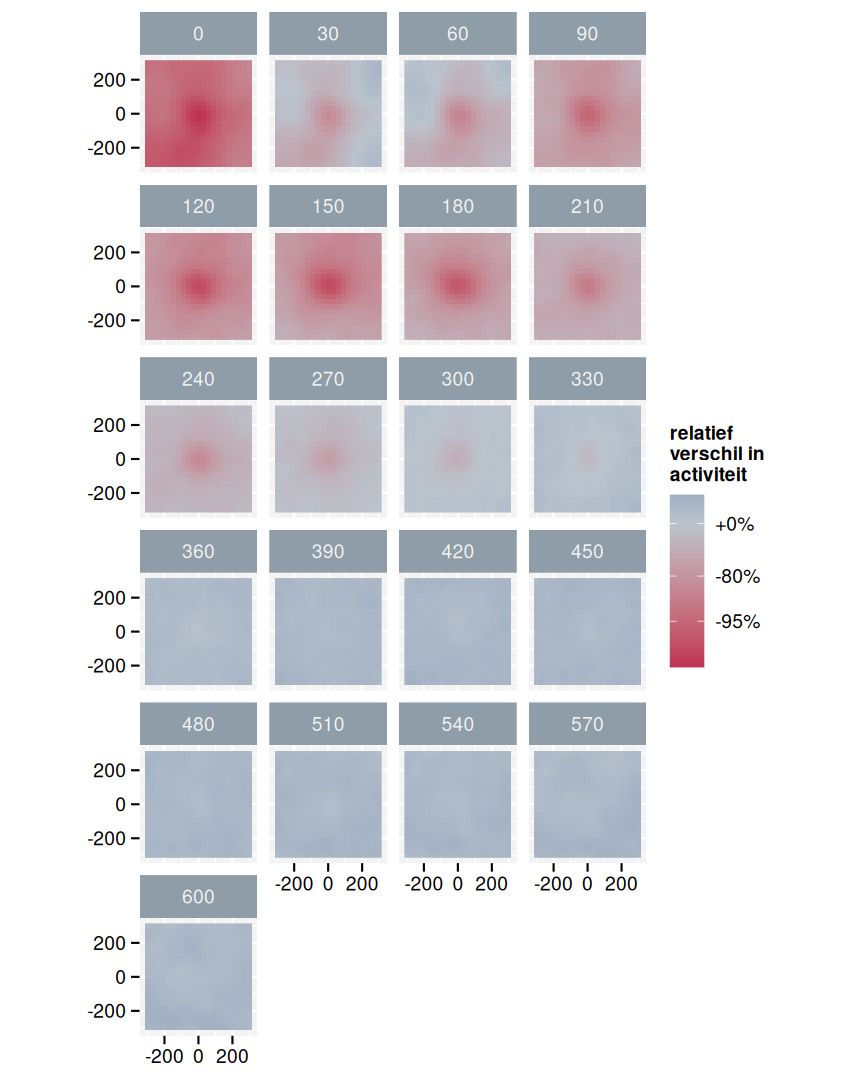
Aangezien de ruimtelijke patronen rond de windturbines (fig. 3.6) en controle (fig. 3.11) sterk van elkaar verschillen, hoeft het niet te verbazen dat het verschil tussen beide patronen (fig. 3.13) op zich eveneens een sterk patroon vertoont. Boven 300 m is weinig verschil. Tussen 90 m en 240 m stellen we een sterke afname in relatieve activiteit vast. In figuur 3.14 hebben we de verschillen opgedeeld in een aantal klassen. We verwijzen naar Onkelinx (2024) voor meer uitleg over deze indeling. De rode zones geven de gebieden met een statische significante afname weer, de groene zones een statisch significante toename.

Figuur 3.13: Relatief verschil in gemiddelde activiteit rond windturbine versus de controle. Afname impliceert minder activiteit rond windturbines in vergelijking met de controlepunten.

Figuur 3.14: Classificatie relatief verschil in gemiddelde activiteit rond windturbine versus de controle.
In figuur 3.15 geven we het verschil wanneer we rekening houden met alle effecten, behalve dat van de individuele windturbine. We combineren met andere woorden het globaal gemiddelde, het hoogte-effect en het ruimtelijke patroon. Op lage hoge is bijna overal een sterke afname van de relatieve activiteit (fig. 3.16). Het effect van de positie van de windturbine ter hoogte van het rotorvlak is nog steeds zichtbaar.
Figuur 3.15: Relatief verschil in gemiddelde activiteit rond windturbine versus de controle.

Figuur 3.16: Classificatie relatief verschil in gemiddelde activiteit rond windturbine versus de controle. Afname impliceert minder activiteit rond windturbines in vergelijking met de controlepunten.
Referenties

